Deduplication - 학습 데이터에서 중복 제거하기
Luda Gen 1.5 모델을 학습할 때 데이터셋에서 중복을 제거한 방법에 대해 이야기합니다.
개요
스캐터랩은 루다가 더 말을 잘 하도록 만들기 위해 많은 노력을 기울이고 있습니다. 그중 루다의 두뇌(?)라고 볼 수 있는 인공지능 모델을 업그레이드하는 프로젝트에도 많은 시간과 노력을 투자하고 있는데요.
그런 방향성에 맞추어 22/4Q 분기에는 Luda Gen 1 모델보다 뛰어난 모델을 학습하기 위한 프로젝트를 진행하였습니다. 이름하여 메가스터디 프로젝트.
메가스터디 프로젝트는 데이터 형식의 기획과 정제부터 시작하여 모델의 학습까지 성공적으로 마치는 것을 목표로 한 거대한 프로젝트였습니다. 학습 시키는 모델이 크기가 큰 모델(LLM, Large Language Model)이었기 때문에 “큰 모델” + “학습”이라서 메가스터디라는 이름이 붙게 되었죠 ㅎ.
아무튼 프로젝트에서 목표로 하는 모델은 Luda Gen 1 모델에 비해 파라미터 개수(= 모델의 크기), 데이터셋 크기, 입력 최대 길이, 프롬프트 형식 등 많은 부분에서 개선이 이루어진 모델이었습니다.
이 모델이 현재 루다를 구동하고 있는 모델이고 Luda Gen 1.5 모델이라고 부르게 됩니다.
Luda Gen 1.5 모델의 학습을 위해 구성한 데이터셋에는 Luda Gen 1 모델 때와는 다르게 외부 문서에서 수집한 언어 데이터들도 포함이 되었는데요. LLM의 학습의 트렌드를 팔로잉 했을 때 데이터의 양과 종류가 다양해지는 것 자체가 학습에 긍정적인 영향을 미칠 것이라고 판단되기도 하였고, 한편으로는 루다가 대화 데이터에서 배울 수 없었던 일반 상식들을 배울 수 있을 것이라는 기대도 있었기 때문입니다. 저희는 이런 이유들을 바탕으로 외부 언어 데이터들도 적극적으로 수집/정제하게 되었습니다.
아무래도 다양한 출처에서 외부 데이터를 수집하였기 때문에 서로 중복된 문서가 있을 것이 분명해 보였습니다. 하지만 전체 데이터셋의 크기가 굉장히 커서 어떤 종류의 문서가 어떤 비율로 중복되었는지 파악하고 그 비율을 원하는 대로 조절하는 것은 굉장히 어려운 일이었습니다.
그러는 한편, “Deduplicating Training Data Makes Language Models Better”라는 논문에는 (제목이 의미하는 바 그대로) 학습 데이터셋 내의 중복을 제거하면 성능이 오른다는 연구가 실려있었기 때문에 저희도 이 논문에서 한 것처럼 깔끔하게 중복을 제거해버리자는 의사결정을 하게 되었습니다.
편집 거리 유사도
우선 “문서가 중복된다”라는 말의 의미를 명확히 해보도록 하겠습니다. 두 문서가 완전히 일치해야 두 문서가 중복된 문서라고 볼 수 있겠죠? 그렇지만 현실에서는 문서가 웹상에서 재가공 되거나 수집이 되는 과정에서 높은 확률로 노이즈가 생기게 됩니다. 그렇기 때문에 적당한 노이즈를 차이를 감안하여 두 문서가 “거의” 일치하는 경우에도 두 문서를 중복으로 보고자 합니다.
“거의” 일치한다는 개념을 명확하게 정의하기 위해 먼저 편집거리 유사도라는 개념을 소개할 필요가 있습니다.
먼저 두 문서의 편집 거리란 한 쪽 문서에서 최소 몇 글자를 삽입(Insertion) 혹은 삭제(Deletion), 치환(Substitution) 해야 다른 문서를 만들 수 있는지를 의미합니다.
삽입은 그냥 내가 원하는 글자를 한 쪽 문서에 추가하는 행위이고 삭제는 말 그대로 글자를 삭제하는 것, 치환은 글자를 원하는 글자로 바꾸는 행위입니다. 더 쉬운 이해를 위해서 간단한 예시를 같이 알아보겠습니다.
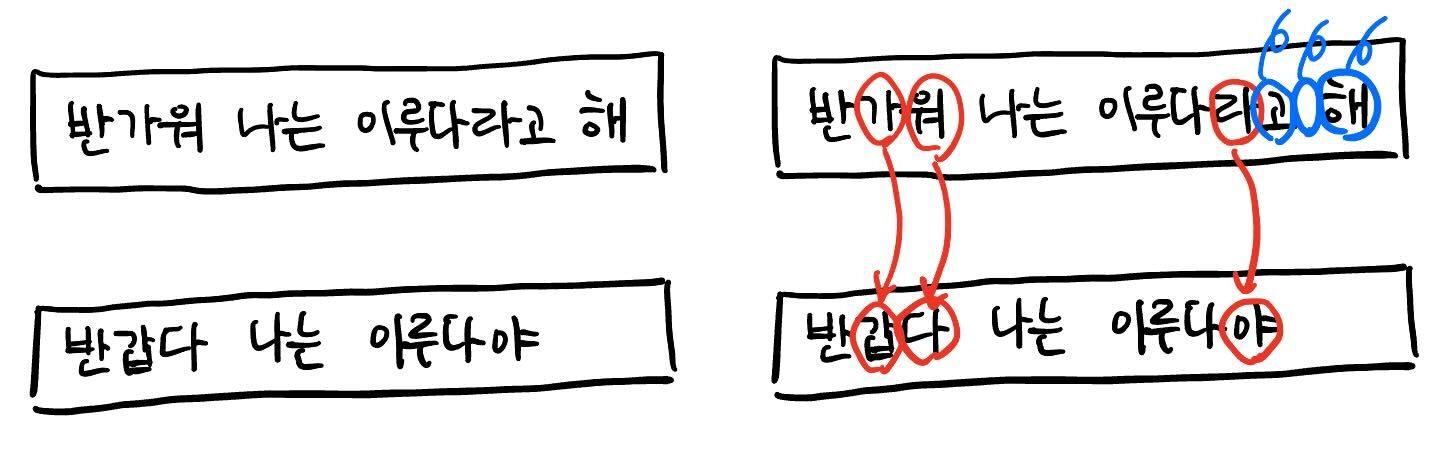
위의 예시의 문서 1에서 “반가워”의 “가”와 “워”를 각각 “갑”과 “다”로 치환하고 “이루다라고 해”의 “라”를 “야”로 치환한 뒤 띄어쓰기와 “고”, “해”를 삭제하면 문서 2와 같아지기 때문에 문서 1과 문서 2의 편집 거리는 삽입, 삭제, 치환한 글자 수를 모두 합한 6이 됩니다.
여기서 편집 거리 유사도는 아래의 수식을 통해 계산되는 값으로 전체 중 얼마큼의 비율이 편집되지 않고 보존되는가를 의미합니다. 위의 예시에서는 문서 1의 길이가 14(띄어쓰기까지 포함한 길이)로 더 길기 때문에 두 문서의 편집 거리 유사도는 \(1 - 6 / 14 = 8 / 14\) 이 됩니다.
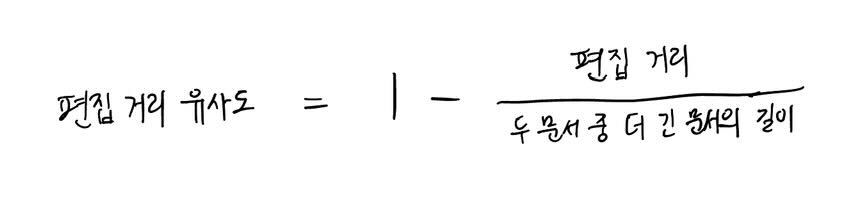
저희는 편집 거리에 따른 문서의 유사성을 정성적으로 판단해 보았고 그 결과를 토대로 편집 거리 유사도가 0.8 이상인 경우에 두 문서를 중복으로 판단하자고 결정하였습니다.
중복 제거의 어려움
편집 거리를 구하는 알고리즘은 시간이 꽤나 오래 걸립니다. 정확히는 두 문서의 길이를 각각 \(L_1\), \(L_2\)라고 했을 때 \(L_1 L_2\) 만큼의 연산량이 필요한 알고리즘이죠.
이걸 모든 문서 쌍에 대해 수행한다고 하면 굉장히 큰 연산량이 필요한데요. 정확히는 문서의 길이 총합을 \(L\)이라고 했을 때, \(L^2\)의 연산량이 들게 됩니다.
(수식 주의: 아래의 식은 모든 문서 쌍마다 문서 길이의 곱만큼 연산량이 필요하다면 전체 연산량은 문서 총 길이의 제곱임을 보여주는 식입니다.)
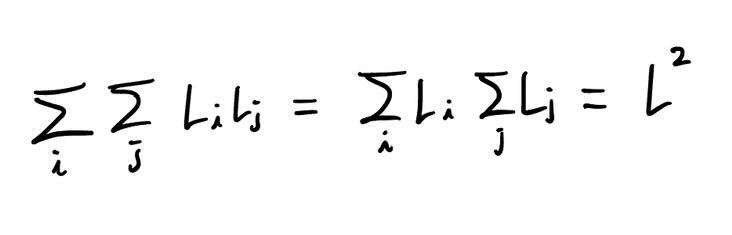
저희의 데이터의 경우 $L$ 값이 이미 알아본 것만 해도 1억보다 훨씬 큰 것으로 집계되었기 때문에 \(L^2\)이라는 연산량은 현실적으로 말이 안 되는 크기였습니다. 그렇기 때문에 이런 나이브 한 방식은 저희처럼 대규모 언어 데이터에 대해서 중복 제거를 하기에는 적절하지 않았습니다.
NearDedup 알고리즘
“Deduplicating Training Data Makes Language Models Better” 논문에서는 위에서 알아본 어려움을 해결하기 위해 NearDedup 이라는 알고리즘을 제안하였습니다.
NearDedup 알고리즘의 요지는 중복일 가능성이 매우 높은 문서 쌍들에 대해서만 실제로 편집 거리를 계산하자는 것입니다. 편집 거리를 계산하는 것이 시간적인 비용이 많이 드는 작업이기 때문에 신중하게 고르자는 것이죠. 중복일 가능성이 매우 높은 문서 쌍을 찾기 위해서 여러 가지 방법으로 문서 쌍을 추리고 마지막에 편집 거리를 계산합니다.
저와 함께 NearDedup 알고리즘을 단계적으로 알아보도록 할게요.
알고리즘은 LSH 알고리즘을 통해서 1차적으로 비교해 봐야 할 문서 쌍을 대폭 줄입니다. LSH 알고리즘이 뭐냐고요? 자세한 내용은 아래의 자료를 참고해 주세요.
여기서는 LSH 알고리즘의 역할을 간단하게 소개하고 넘어가도록 하겠습니다. LSH 알고리즘은 입력으로 문서들이 주어지면 그것들 중 유사할 가능성이 높은 문서들을 그룹으로 묶어서 반환해 주는 알고리즘입니다.
따라서 우리는 LSH 알고리즘의 결과로 나온 각각의 그룹들에 대해서 그룹 내에 있는 문서들에 대해서만 서로 중복인지를 비교해 주면 되는 겁니다. 이 알고리즘을 수행하면 전혀 유사하지 않은 문서 쌍을 비교하게 되는 비효율적인 작업은 하지 않아도 된다는 것이 장점이죠.
자, 그럼 이제 LSH 알고리즘을 통해서 비교해 봐야할 문서쌍이 대폭 줄었다는 것을 알 수 있습니다.
NearDedup 알고리즘은 여기서 그치지 않고 자카드 유사도라는 개념을 사용해서 한 번 더 비교할 문서 쌍을 필터링합니다. 자카드 유사도라는 개념이 익숙하지 않으실 분들을 위해 간단하게 설명하자면, 자카드 유사도는 두 문서에 등장하는 단어 집합을 각각 A, B라고 했을 때, 아래와 같은 수식으로 구해지는 값입니다.
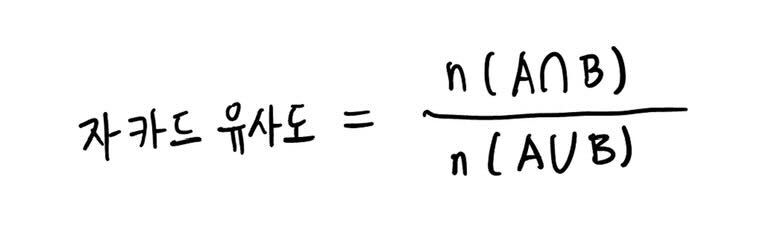
두 문서가 완전히 동일하다면 자카드 유사도는 1이 된다는 것을 알 수 있죠. 또 두 문서에 겹치는 단어가 하나도 없을 정도로 문서가 다르다면 자카드 유사도는 0이 되겠고요. 문서의 유사성을 판단하는 하나의 지표라고 생각하시면 됩니다.
NearDedup 알고리즘에서는 살아남은 문서 쌍들 중에서 자카드 유사도가 특정 값 이상인 쌍들에 대해서만 편집 거리를 계산합니다. 이 특정 값은 유사한 문서들과 유사하지 않은 문서들의 자카드 유사도를 비교해본 뒤에 0.8로 정하였습니다.
이제 문서의 쌍들이 두 번의 필터링을 거치며 많이 줄어들었을 겁니다. 이렇게 필터링을 거치고도 살아남은 문서의 쌍들은 중복일 가능성이 아주 높은 쌍들이라고 볼 수 있겠죠.
이제 이런 문서 쌍들에 대해서 마침내 편집 거리 유사도를 계산해 줍니다. 그리고 편집 거리 유사도가 0.8 이상으로 나온 문서 쌍 중에 더 긴 문서를 데이터에서 날리면 끝입니다.
왜 더 긴 문서를 날리냐고요? 저희의 데이터들에서 중복인 케이스들을 살펴보면 아래의 예시처럼 문서의 중간중간에 광고 문구 같은 노이즈가 추가된 케이스가 대부분이었습니다. 따라서 이런 케이스들을 손쉽게 다루기 위해 그냥 중복인 문서들의 그룹에서 가장 짧은 문서만 살아남도록 하는 알고리즘을 구성하게 되었습니다.

요약하면,
- LSH 알고리즘으로 유사할 가능성이 높은 문서들을 그룹으로 묶는다.
- 각각의 그룹 안에 있는 모든 문서 쌍에 대해 자카드 유사도를 계산한다.
- 자카드 유사도가 0.8 이상인 문서 쌍들에 대해서 편집 거리 유사도를 계산한다.
- 편집 거리 유사도가 0.8 이상인 문서 쌍에 대해 더 긴 문서를 데이터셋에서 삭제한다.
와 같이 서술할 수 있습니다.
이 알고리즘의 결과로 중복인 문서들은 사라지고 깔끔한 데이터셋을 얻을 수 있었어요. 😀
구현
위의 알고리즘은 각각의 과정마다 병렬적으로 처리될 수 있는 알고리즘입니다. 따라서 아파치 빔을 사용하면 알고리즘을 수행하는 속도를 비약적으로 끌어올릴 수 있게 됩니다. 아파치 빔으로 어떻게 속도를 비약적으로 끌어올리는지 자세히 알고 싶으시다면 아래의 블로그를 참고해주세요.
Apache Beam으로 머신러닝 데이터 파이프라인 구축하기 1편 - 도입과 사용
Apache Beam으로 머신러닝 데이터 파이프라인 구축하기 2편 - 개발 및 최적화
아래의 코드는 위에서 설명한 과정들을 아파치 빔을 사용해 구현한 것입니다.
class LSHAlgorithm(beam.DoFn):
"""
주어진 문서의 MinHash 값을 계산하고 해쉬 백터를 ```b```개의 버킷으로 나누어 각각을 문서의 key 값으로 사용합니다.
따라서 입력으로 들어온 문서 하나당 ```b```개의 (key, 문서) 쌍을 반환합니다.
:param b: 버킷의 개수
:param num_perm: MinHash의 차원
:param seed: MinHash를 구할 때 사용할 랜덤 시드 값
"""
def __init__(self, b: int, num_perm: int, seed: int = 42):
self.b = b
self.num_perm = num_perm
self.seed = seed
def process(self, item: Dict[str, Any]) -> List[Any]:
document_text = item["contents"]
# min hash 계산
min_hash = MinHash(num_perm=self.num_perm, seed=self.seed)
min_hash.update(document_text)
# 버킷 나누기
lsh = LSH(b=self.b, num_perm=self.num_perm)
lsh.insert(document_text, min_hash)
for (start, end), H in zip(lsh.hashranges, lsh.keys[document_text]):
yield [(start, end, H), item]
class PairUpDocument(beam.DoFn):
"""
버킷 해쉬가 같은 문서들의 목록이 입력으로 들어오면 두 개를 골라 쌍을 반환합니다.
"""
def process(self, item: Tuple[Any, Iterable[Dict[str, Any]]]) -> Iterable[List[Dict[str, Any]]]:
documents = item[1]
for i in range(len(documents)):
for j in range(i, len(documents)):
yield [documents[i], documents[j]]
class CheckDuplication(beam.DoFn):
"""
입력으로 받은 두 문서가 서로 중복인지 검사합니다.
"""
def __init__(
self,
jaccard_threshold: float = 0.8,
edit_threshold: float = 0.8,
):
self.jaccard_threshold = jaccard_threshold
self.edit_threshold = edit_threshold
def process(self, item: List[Dict[str, Any]]) -> List[Tuple[str, Tuple[Dict[str, Any], bool]]]:
document_id1 = item[0]["data_id"]
document_id2 = item[1]["data_id"]
document_text1 = item[0]["contents"]
document_text2 = item[1]["contents"]
if document_id1 == document_id2:
return [(document_id1, (item[0], True)), (document_id2, (item[1], True))]
if jaccard_similarity(document_text1, document_text2) <= self.jaccard_threshold:
# 두 문서는 서로 중복이 아닙니다.
return [(document_id1, (item[0], True)), (document_id2, (item[1], True))]
if edit_similarity(document_text1, document_text2) <= self.edit_threshold:
# 두 문서는 서로 중복이 아닙니다.
return [(document_id1, (item[0], True)), (document_id2, (item[1], True))]
# 두 문서가 중복으로 판별되면 더 긴 문서를 제거합니다.
return (
[(document_id1, (item[0], True)), (document_id2, (item[1], False))]
if len(document_text1) < len(document_text2)
or (len(document_text1) == len(document_text2) and document_id1 < document_id2)
else [(document_id1, (item[0], False)), (document_id2, (item[1], True))]
)
class Deduplicate(beam.DoFn):
def process(self, item: Tuple[Any, Iterable[Tuple[Dict[str, Any], bool]]]) -> List[Dict[str, Any]]:
documents = item[1]
alive = True if False not in [document[1] for document in documents] else False
return [documents[0][0]] if alive else []
corpus = (
corpus
| "LSHAlgorithm"
>> beam.ParDo(
LSHAlgorithm(b=args.num_bucket, num_perm=args.num_perm)
)
| "GroupByBucket" >> beam.GroupByKey()
| "PairUpDocument" >> beam.ParDo(PairUpDocument())
| "ReshufflePair" >> beam.Reshuffle()
| "CheckDuplication"
>> beam.ParDo(
CheckDuplication(
jaccard_threshold=args.jaccard_threshold,
edit_threshold=args.edit_threshold,
)
)
| "GroupByDocumentID" >> beam.GroupByKey()
| "Deduplicate" >> beam.ParDo(Deduplicate())
)