꼼꼼하고 이해하기 쉬운 Reformer 리뷰

Review of Reformer: The Efficient Transformer

구상준 | 2020년 04월 29일 | #Machine_Learning

이번 ICLR 2020에서는 여러 특기할 만한 구조들이 제안되었습니다. 그 중에서 저희가 인상깊게 본 구조는 구글에서 제안한 Reformer입니다. 기존의 Transformer 구조는 데이터 토큰이 조금만 많아져도 모델 크기가 엄청나게 커지는 문제가 있었습니다. 이는 Attention 모델이 데이터 열에서 모든 데이터 포인트 쌍 간의 가중치를 나타내기 때문입니다. 이 포스트에서는 Reformer의 이론적 배경과 이를 바탕으로 구축된 구조를 살펴보며, 이 문제를 어떻게 완화했는지 따져보고자 합니다.

들어가며: Transformer 구조와 이로 인한 메모리 문제
이론적 배경
1. Locality-Sensitive Hashing
2. Reversible-Network
모델 구조
실험 결과
1. 데이터셋 및 실험설계
2. 가설검증을 통한 결과 분석
글을 마치며
Reference
Appendix
1. 구면으로 사상할 때 임베딩의 크기 정보가 손실되는 문제에 대해서
2. LSH Attention의 유효성에 대해서

들어가며: Transformer 구조와 이로 인한 메모리 문제

Reformer의 구조를 살펴보기 전에 Transformer의 구조를 간단히 살펴봅시다. (Transformer에 대한 자세한 설명은 저희 블로그 포스팅을 참조하여 주십시오.) Transformer는 Scaled-dot Product Attention이라는 Attention Layer와 이를 다른 공간으로 사상하는 Feed-Forward Layer의 Residual Connection N층으로 구성되어 있습니다.

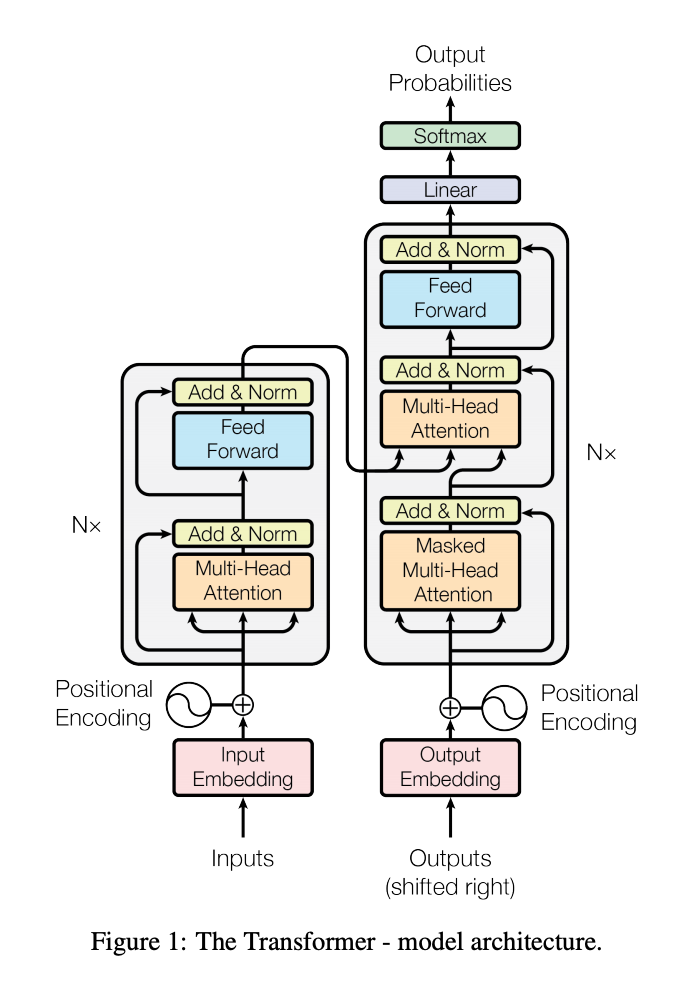
기존의 Transformer에서 다루었던 번역이나 언어 이해 문제의 경우 문장이나 문단의 길이가 그렇게 길지 않았기 때문에 구조가 커지는 것이 큰 문제가 되지 않았습니다. 실제로 원 Transformer과 BERT에서 다루는 개수는 512개에 불과했는데 그 정도로도 문장이나 문단을 담는 것에 충분하였기 때문입니다. 그렇지만 이것보다 더 큰 데이터 (예를 들어서 문서 단위의 언어 데이터나 이미지 데이터 등)을 다루게 되면 문제가 심각해집니다.

Attention 구조에 의한 메모리 문제

Transfomer의 메모리 문제는 근본적으로 Scaled dot-Product Attention 구조에서 비롯됩니다. Scaled dot-Product Attention 구조에서 단어 A에 단어 B 가 주는 가중치는 다음 세 개의 변수로 표현할 수 있습니다.

Query (Q): 영향을 받는 단어 A를 나타내는 변수입니다.
Key (K) : 영향을 주는 단어 B를 나타내는 변수입니다.
Value (V) : Key에 대응되는 영향력 값입니다.

이 경우, 가중치 합은 다음과 같이 나타납니다.

\[\text{Attention}(Q,K,V) = \text{softmax}({\frac{Q{K^{T}}}{\sqrt{d_{k}}}})V\]

이 수식에 따르면 Attention 구조의 시간복잡도는 Q의 크기와 K의 크기의 곱에 비례합니다. Q와 K는 데이터 열의 길이와 크기가 같으므로 데이터 열의 길이(한번에 들어오는 데이터 토큰의 수)의 제곱에 비례한다는 것을 의미합니다. 데이터의 길이가 10배 길어지면 100배 큰 구조가 필요한 셈입니다. 이 수식은 원 Transformer 구조를 문서 단위의 긴 입력에 대해 확장시키는 것에 근본적으로 한계가 있음을 시사합니다.

Feed Forward Layer에 의한 메모리 문제

비록 메모리 문제의 상당한 부분은 Attention 구조에서 비롯된 것이지만, 다른 구조들도 마찬가지로 비슷한 문제를 나타냅니다. Transformer는 Attention과 Feed Forward Layer가 결합한 구조로 구성되는데, Feed Forward Layer는 단순한 선형곱 연산으로 나타낼 수 있습니다.

\[\text{FFN}(x) = max(0, x \cdot W_{1} + b_{1})\cdot W_{2} + b_{2}\]

이 Feed Forward Layer는 각 Attention Layer의 출력에 모두 적용이 되어야합니다. 즉, 이 구조가 차지하는 메모리는 데이터 열의 길이와 해당 Layer의 입출력 차원의 곱에 비례합니다. 문제는 보통 이 때 사용되는 입출력 차원은 대개의 경우, 모델 임베딩의 차원에 비해 크다는 점입니다. 예를 들어 원 Transformer 논문에서 제안된 토큰의 최대 개수는 512개 였습니다만, 내부 Feed Forward Layer의 입출력은 그 네 배인 2048차원이었습니다. 입력 차원이 크기 때문에 데이터 길이가 충분히 길면 이 Feed Forward 구조가 차지하는 메모리도 무시할 수 없게 됩니다.

N-stacked Residual Connection에 의한 메모리 문제

Torch와 Tensorflow 등의 머신러닝 프레임워크에서 미분값을 계산하는 방법은 다음과 같습니다.

클래스로 정의된 계산 흐름에 따라 입력 데이터에 대해서 출력값을 계산합니다. 모델에 입력이 전달될 때, 어떤 입력이 들어와서 어떤 출력이 생성되었는지 기록합니다.
종점부터 시작점까지 거슬러 올라가며, 각 모델의 출력값과 이에 대응되는 입력값을 사용해 미분값을 근사한 수치를 계산합니다.

컴퓨터가 근삿값을 계산하려면 입력과 그에 대한 출력값이 필요합니다. 그 때문에 구조가 복잡하면 입력과 출력을 저장하기 위한 메모리가 많이 사용됩니다. Transformer는 N층으로 Attention Layer와 Feed-Forward Layer가 결합돼 있으므로, 중간 결과를 저장하는 데 N배에 달하는 메모리가 필요합니다.

논문이 기여한 부분

논문이 기여한 부분은 크게 3가지로 요약됩니다.

서로 비슷한 쌍만 Attend 한다: 나폴레옹 자서전을 예로 들어 봅시다. 이 책에서 “나폴레옹”이라는 단어와 연관성/영향력이 높은 단어를 따져보면 “프랑스”, “황제”, “전쟁” 등이 될 것입니다. 이에 비해 “이동했다”, “집을”, “찾아” 같은 단어는 빈도는 높지만 영향력이 미미할 것입니다. 만약 영향력이 높은 단어 쌍끼리만 가중치를 계산할 수 있다면 성능 저하 없이 복잡도가 대폭 줄어든 구조를 얻을 수 있을 것입니다. 본 논문의 저자들은 1) 영향력이 높은 단어 쌍은 임베딩 공간에서 서로 비슷한 쌍이며 2) 이런 쌍들은 Locality-Sensitive Hashing (LSH)을 이용해서 빠르게 찾을 수 있다는 점을 지적합니다.
Chunking을 이용해 메모리를 줄인다: Feed-Forward Layer는 Attention Layer와 다르게 데이터 포인트의 위치에 무관하게 계산됩니다. 따라서 데이터 포인트들을 묶어줄 수 있다면 계산하는 단위를 나눌 수 있고 전체 데이터 포인트에 대한 Feed-Forward Layer의 가중치를 한번에 메모리에 올리지 않아도 됩니다.
Reversible Layer를 이용해 메모리를 줄인다: Transformer는 Attention Layer와 Feed-Forward Layer의 Residual Connection으로 되어있습니다. Residual Connection (잔차 연결)은 F(x) = x + G(x) 형태로 나타나는 연결을 뜻합니다. Gomez et al.은 2017년 수식을 살짝 변형해 출력을 이용해서 입력을 다시 복원할 수 있는 형태로 기술했습니다. 출력으로 입력을 복원할 수 있으므로, 각 중간 단계의 입출력을 저장할 필요 없이 바로 출력에서 미분값을 계산하여 훈련할 수 있습니다.

논문 자체의 구조는 어렵지 않지만 다른 연구에서 차용한 부분이 많다보니 배경지식이 없으면 이해하기 어렵습니다. 따라서 논문에서 사용한 두 개의 중요한 알고리즘인 LSH와 Reversible Network를 먼저 다루고, 논문에서 어떻게 활용하는지 설명하겠습니다.

이론적 배경

Locality-Sensitive Hashing

Hashing은 임의의 데이터를 길이가 고정된 값(해시값 또는 해시열쇠값)에 사상하는 것을 의미합니다. 데이터를 미리 Hashing 해두면 Hash 값만으로 쉽게 데이터를 찾을 수 있습니다. 이와 관련된 실제 예시는 우리 주변에서도 쉽게 찾아볼 수 있습니다. 주민등록번호는 국민 개개인의 Hash값이고, 핸드폰 전화번호는 통신사에 연결된 핸드폰의 Hash값입니다. 구글에서 제공하는 URL 짧게 줄여주는 서비스인 bitly 에서 만들어주는 주소도 URL 주소의 Hash값이라 할 수 있습니다.

보통 Hash값은 연결된 데이터와 전혀 관련이 없을 때가 많습니다. 그렇기 때문에, 전체 데이터 분포에서 데이터의 상대적 위치를 확인하거나 한 데이터와 가장 가까운 다른 데이터를 찾는 등 데이터에 대한 비교 분석을 할 때는 반드시 실제 데이터값을 비교하는 연산이 필요합니다. 이때 가까운 데이터끼리는 가까운 Hash값을 갖도록 구성할 수 있다면 비교하는 연산을 Hash값에 대한 연산으로 근사할 수 있습니다. 가까운 값들끼리 가까운 Hash값을 가지도록 Hashing하는 방법을 Locality-Sensitive Hashing이라 부릅니다. 아주 정확한 예시는 아니지만 우리 주변에서는 우편번호를 예로 들 수 있습니다. 우편번호는 가까운 지역일수록 비슷하게 설계되었습니다. 따라서 정확한 주소를 몰라도 우편번호가 같다면 비슷한 지역에 모여있으리라 예상할 수 있습니다.

문제는 어떻게 Locality-Sensitive Hashing을 기계적으로 수행할 수 있을지입니다. 한 가지 방법은 사상법(Projection Method, 2000)입니다. 주어진 데이터를 임의의 평면으로 구분짓는다고 가정해봅시다. 그러면 데이터는 평면 한 쪽과 다른 쪽으로 구분될 것입니다. 요점은 비슷한 위치에 있는 데이터들은 같은 편에 설 가능성이 높다는 것입니다. 따라서 임의의 평면들에 계속해서 사상했을 때, 각 평면에 사상했을 때 부호값은 Locality-Sensitive Hash가 될 수 있습니다.

Reformer에서는 조금 다른 방식인 Angular LSH를 사용합니다. 이 방법은 방향 성분만을 활용하여 Hash 값을 생성합니다.

전체 데이터 포인트들의 벡터를 단위 구면에 사상합니다. 이렇게 사상하게 되면 전체 데이터 포인트를 오직 각도만 사용해서 기술할 수 있습니다. (반지름 1인 구면좌표계를 생각해봅시다.)
이제 각 각도가 어느 사분면에 있는지 확인해봅시다. 눈치가 빠르신 분들은 “비슷한 데이터들은 같은 사분면에 있다”는 점을 포착하셨을 것입니다. 따라서 사분면의 번호를 Hash값으로 사용한다면, 비슷한 데이터들을 가깝게 구성할 수 있습니다.
이제 사상한 구면을 필요한 만큼 임의로 회전시킵니다. (이미지에서는 이해를 돕기 위해서 대신 사분면을 회전시켰습니다.) 데이터가 가까우면 가까울수록 전체 Hash값을 공유할 가능성이 높아지고, 충분히 많은 Hash값을 사용하면 데이터를 구별하는 변별력이 생깁니다.

예시를 들어서 설명해봅시다. 2차원 임베딩 벡터 X1=(3,4), X2=(-12,5)가 있다고 가정해보겠습니다. 이를 반지름 1인 구에 사상하면 그 사상점은 X1’=(3/5, 4/5), X2’=(-12/13, 5/13)이 됩니다. 이제 원을 돌려보면서 몇 사분면에 있는지 확인하는데 편의상 원 대신 좌표계를 돌리겠습니다. 그림을 보면 좌표계가 회전함에 따라 빨간 점과 파란 점이 각각 위치하는 사분면이 달라짐을 알 수 있습니다. 이 경우, X1의 Hash값은 (1, 4, 2) X2의 Hash값은 (2, 2, 3)이 됩니다.

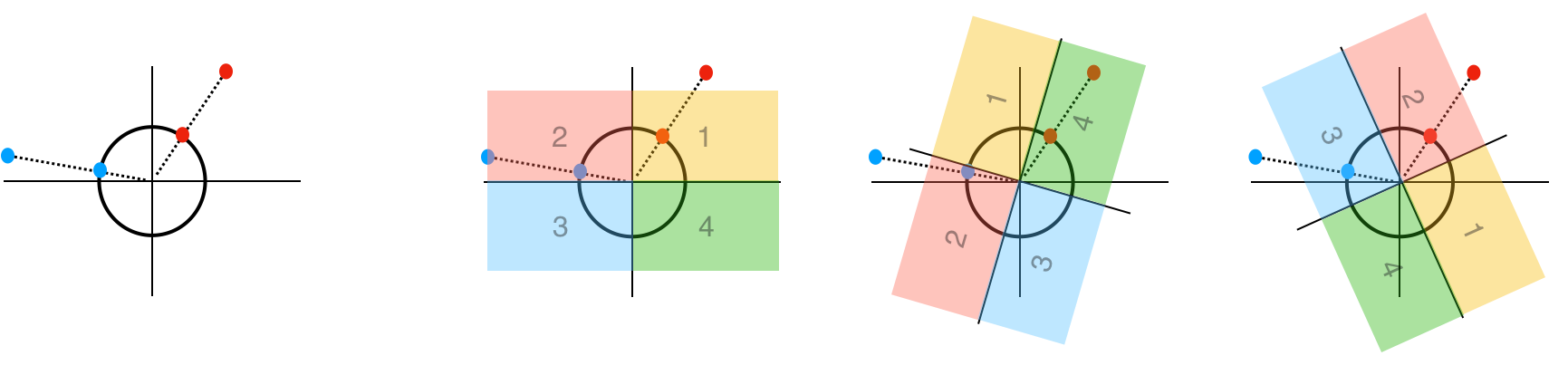
이제 임의의 벡터 Y=(4,3)가 주어졌다고 가정해 봅시다. 이 경우, 사상점 Y’은 (4/5, 3/5)에 위치합니다. 똑같이 원을 돌리면서 Hash값을 표현해보면 Y의 Hash값은 (1, 4, 2)가 됩니다. 이 값은 X1의 Hash값과 같고 X2의 Hash값과는 다르므로 데이터 간의 직접 비교 연산 없이 Hash값이 일치하는지 보는 것만으로도 가까운 점들을 선별할 수 있는 것입니다.

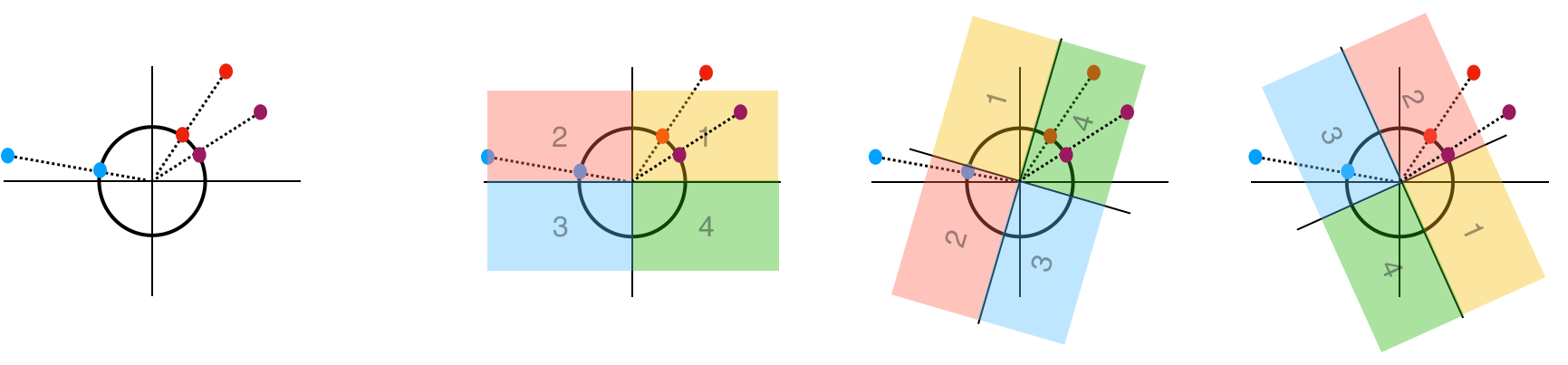
눈치가 빠른 분들은 “이렇게 데이터를 저장하면 방향 값은 살아있어도 변위값이 손실되지 않나?”라고 생각하실 수 있습니다. 이것에 대해서는 Appendix의 구면으로 사상할 때 임베딩의 크기 정보가 손실되는 문제에 대해서를 참조해주시기 바랍니다.

Reversible Network

다음은 Gomez et al.이 2017년에 제안한 Reversible Layer입니다. 이는 원래 이미지 처리에 사용되는 ResNet 구조에서 메모리를 효율적으로 사용하기 위해 고안되었습니다. 기존의 ResNet에서 사용되는 계산 블록은 다음과 같이 하나의 입력에서 하나의 출력이 나오는 구조입니다.

\[y = x + F(x)\]

이 식으로 계산하면, x에서 y를 계산할 수는 있어도 y에서 x를 역으로 계산해낼 수는 없습니다. Gomez는 계산에 들어가는 입력 x와 출력 y를 ($x_{1}$,$x_{2}$)와 ($y_{1}$,$y_{2}$) 쌍 형태로 기술해보았습니다.

\[y_{1} = x_{1} + F(x_{2}), y_{2} = x_{2} + G(y_{1})\]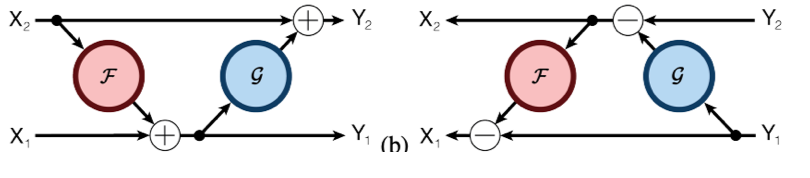

이렇게 되면 $y_{1}$, $y_{2}$가 주어졌을 때, $x_{2} = y_{2} - G(y_{1})$로 역산할 수 있고 $x_{1} = y_{1}-F(x_{2})$로 역산할 수 있습니다. 즉, ResNet의 각 블록을 이 같은 형태로 치환하면, 임의의 시점의 출력값을 토대로 그 출력에 대한 입력값을 표현할 수 있습니다. 따라서 중간 결과를 저장할 필요가 없이 Forward 연산을 반복적으로 적용해 수치적 미분값을 얻을 수 있게 됩니다.

모델의 구조

LSH Attention 적용하기

먼저 데이터 포인트들에 대해서 Attention 가중치를 계산하기에 앞서 본 논문의 구조에서는 각 데이터 포인트에 Locality Sensitive Hashing을 적용합니다. 요점은 Hash값이 일치하는 데이터에 대해서만 Attention을 계산하는 것입니다. 이를 위해 본 논문에서는 다음 가설을 세웁니다.

\[Query(Q)=Key(K)\]

본 논문에서는 저자들은 각 데이터 포인트를 Q로 사상하는 행렬과 K로 사상하는 행렬을 동일하게 설정하였습니다. 즉, 이 가설에서 Query와 Key는 본질적으로 같은 값입니다. 얼핏 보면 그다지 논리적으로 다가오지 않는 가설입니다. 그러나 논문의 저자들은 데이터셋이 충분히 크다면 이 가설로 구성된 Transformer 구조는 성능이 저하되지 않는다는 것을 보였습니다. 위에서도 말씀드렸다시피 한 문서 내에서 중요한 단어는 얼마 되지 않을 것입니다. 그렇다면 그 단어들은 주는 영향력과 받는 영향력이 모두 클 것이고, 반면 접속사나 관사 등은 그렇지 않을 것입니다.

LSH Attention을 Transformer에 적용하는 절차는 다음과 같습니다.

Q=K이므로 각 데이터 포인트에 대한 Q=K 값을 일렬로 된 벡터 형태로 나타냅니다.

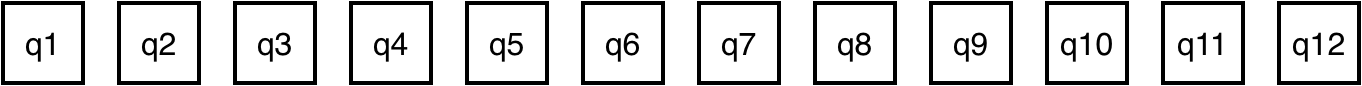
각 데이터 포인트에 LSH를 적용합니다. 그 후 같은 Hash값을 가진 데이터 포인트끼리 버킷으로 묶습니다(Bucketing). 각 Hash 버킷에 임의로 순서를 매겨서 정렬합니다. (이미지 상에는 같은 색깔로 버킷을 표시하였습니다.)

각 버킷에는 높은 확률로 데이터 포인트들이 불균형하게 배당될 것입니다. 따라서 데이터 포인트들을 고정된 크기의 구역으로 분절합니다(Chunking).

이제 Attention Weight를 계산하는데, 다음 조건을 모두 만족하는 쌍들에 대해서만 계산합니다.
1. 두 데이터 포인트가 같은 버킷에 있어야 합니다. (색이 같아야 합니다.)
2. 두 데이터 포인트는 서로 같은 구역에 있거나, Attention의 도착점 데이터 포인트는 시작 데이터 포인트가 있는 구역 바로 앞 구역에 있어야 합니다.
일반적인 Transformer는 각 데이터 포인트들 각각이 스스로를 attend 할 수 있지만, 이 구조에서는 Q=K 를 따르기 때문에 스스로 Attention한 내적값은 다른 Attention 내적값보다 언제나 매우 큽니다. 따라서 이 구조에서는 조건을 만족하는 쌍이 자신으로만 구성되는 경우를 제외하면 스스로를 attend하는 것을 허용하지 않습니다.

같은 부분과 앞 부분에만 접근하므로 각 데이터 포인트가 최대로 attend하는 수는 각 분절된 부분 크기의 두 배만큼입니다. 데이터 포인트의 길이를 $l$이라 하고 분절된 부분의 수를 $c$라 할 때 분절된 부분의 크기는 $l/c$이고 Attention의 수는 $l \cdot {(2l/c)}^{2}$에 비례합니다. $c$가 충분히 크다면 $l$에 선형적으로 비례하는 구조로 간주할 수 있고 이는 원래 Transformer가 모든 쌍을 attend하기 때문에 $l^{2}$에 비례하는 복잡도를 가지는 것을 생각하면 상당히 개선된 것입니다.

Feed Forward Network에 Reversible Network 적용하기

Reversible Network에 대해 위 세션에서 설명하였습니다. 논문의 저자들은 Attention Layer와 Feed Forward Layer가 이루는 블록을 Residual Network로 간주할 수 있으며 따라서 Reversible Network에서와 같이 입출력을 둘로 나눌 수 있음을 보였습니다.

\[y_{1} = x_{1} + F(x_{2}), y_{2} = x_{2} + G(y_{1})\]

이 구조는 바로 Transformer Block에 다음과 같이 적용할 수 있습니다.

\[y_{1} = x_{1} + Attention(x_{2}), y_{2} = x_{2} + FeedForward(y_{1})\]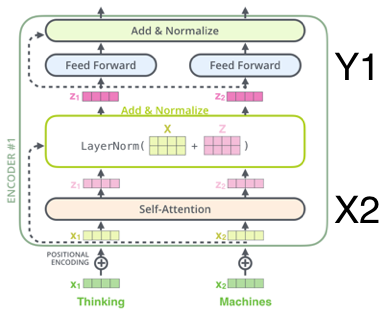

이 구조로 변형한 Transformer는 N층 블록의 결과물을 모두 저장할 필요 없이 한 층에 대해서만 메모리를 사용하여 필요한 연산을 수행합니다. Python 기반의 딥러닝 프레임워크에 익숙하신 분들은 PyTorch나 Tensorflow에서 Backward 연산을 Forward 연산으로 구현하는 형태를 상상해보시기 바랍니다.

Feed Forward Network에 Chunking 적용하기

Feed Forward Layer는 데이터 포인트의 위치와 무관하다고 상술한 바 있습니다. 각 구역으로 나뉜 부분 c에 Feed Forward Layer를 순차적으로 적용하면 하나의 부분에 대한 Feed Forward Layer 분량의 메모리만 필요합니다.

논문의 공간 복잡도와 시간 복잡도를 비교한 표는 이 구조가 얼마나 효율적으로 Transformer구조를 간소화하는지를 알려줍니다. 시간/공간 복잡도 상의 이득 대부분이 길이의 제곱에 비례하는 ttention연산을 길이에 선형으로 비례하는 양의 LSH Attention연산으로 대체하는 데서 비롯됨을 확인할 수 있습니다.

아마 눈치가 빠르신 분들은 지금쯤 이 알고리즘이 효과적으로 작동하기 위해서는 구역의 개수가 충분히 많아야 한다는 사실을 포착하셨을 것입니다. 논문에서는 길이 64K 데이터를 16K 개의 부분으로 분절하는 구조를 제안하였습니다. 즉, 각 분절된 부분의 크기는 매우 작습니다.

실험 결과

데이터셋 및 실험설계

실험에 활용한 데이터셋은 다음 2가지입니다.

imagenet64: 이미지넷 데이터셋은 이미지에 등장한 객체의 종류를 분류하는 작업과 관련있으며 20,000개 이상의 종류 아래 14,000,000 개 이상의 이미지로 구성되었습니다.
enwiki8-64K: enwiki8은 전체 영어 위키피디아 데이터를 압축하는 작업으로 본 논문에서 사용하는 enwiki8-64K는 각 부분이 64K 토큰으로 구성된 데이터입니다.

실험은 Transformer로 입력 데이터를 인코딩한 뒤 다시 디코딩하는 압축 작업으로 이루어지며, 제안한 구조의 성능은 bit-per-dim으로 측정되었습니다. 데이터를 온전하게 표현하기 위한 인코딩 비트가 적으면 적을수록 압축이 효과적으로 되었음을 의미합니다.

가설검증을 통한 결과 분석

제시한 Reformer의 유효성은 다음 세 가설로 정리할 수 있습니다.

Reformer 구조에서 Query는 Key와 같다고 간주해도 무방하다.
Reformer의 Attention Block은 Reversible Layer 형태로 중첩할 수 있다.
LSH Attention을 활용하면 기존 구조의 성능을 크게 저하하지 않으면서 입력 길이에 선형인 시간 복잡도를 보이게 개선할 수 있다.

그 중 가설 3이 가장 중요한 가설로 Reformer의 유효성을 본질적으로 따지는 것이라 하겠습니다.

가설 검증 1: Q=K

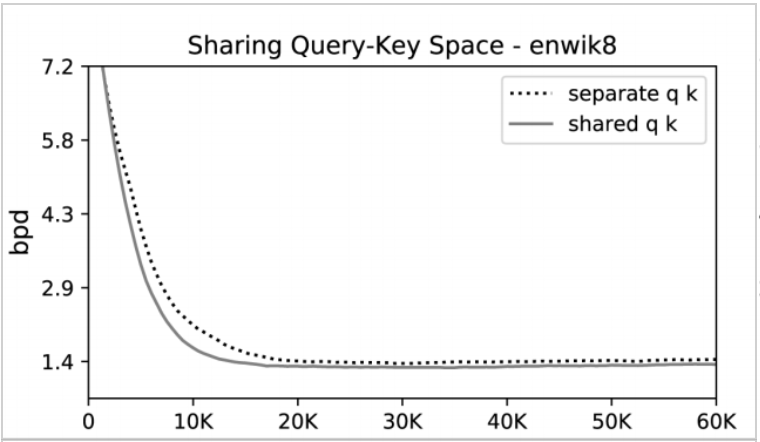
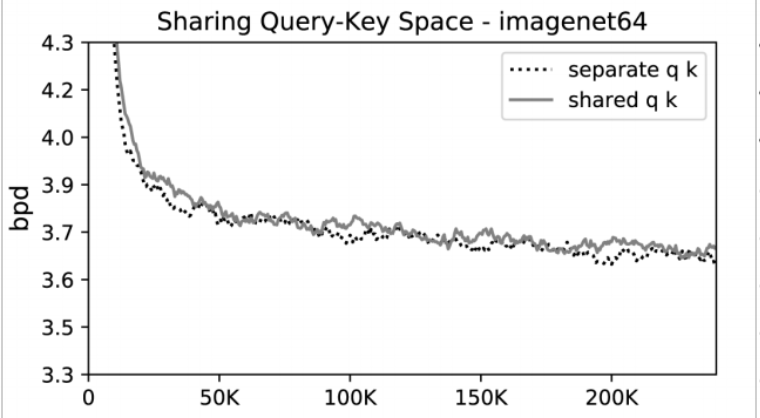
실험 결과, Query와 Key 행렬을 분리한 경우와 그렇지 않은 경우의 성능 차이는 미미했습니다. 오히려 enwiki8 데이터셋에서 Query와 Key를 공유했을 때 더 빠르게 수렴함을 확인할 수 있습니다. 즉, 위의 Query-Key 가설에서 비롯된 구조 변경은 성능에 영향을 주지 않습니다.

가설 검증 2: Reversible Layer의 활용

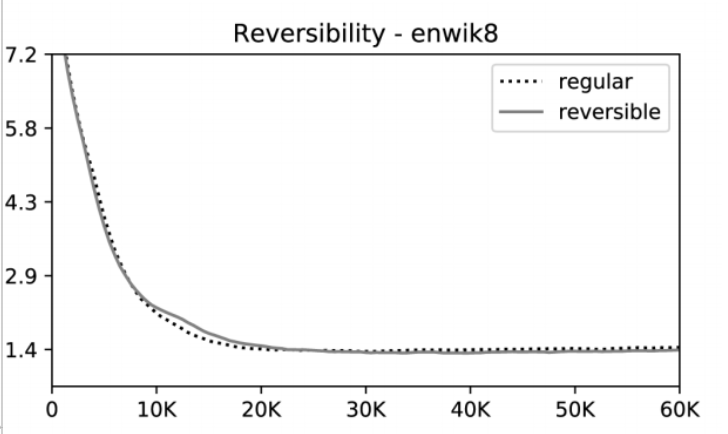
실험 결과, Reversible 형태로 구성한 구조와 그렇지 않은 구조 사이의 성능 차이는 미미하였습니다. 즉, Reversible 구조의 활용은 성능에 영향을 주지 않습니다.

가설 검증 3: LSH Attention의 활용

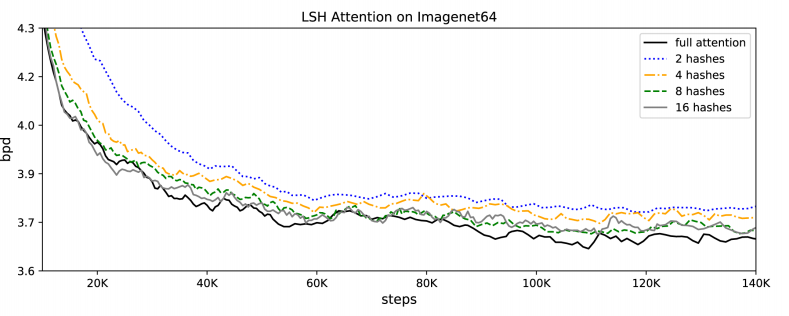
Imagenet64 데이터셋을 사용한 실험 결과에서 병렬적인 Hash를 많이 둘수록 Full Attention을 한 경우와 성능 차이가 줄어드는 것을 확인할 수 있습니다. 아울러 Hash를 8개 이상 두면 Full Attention할 때와 거의 비등한 절대 성능을 보입니다. 저자들은 정확도와 계산량 사이의 경중에 따라 Hash값을 가감할 수 있다고 주장합니다.

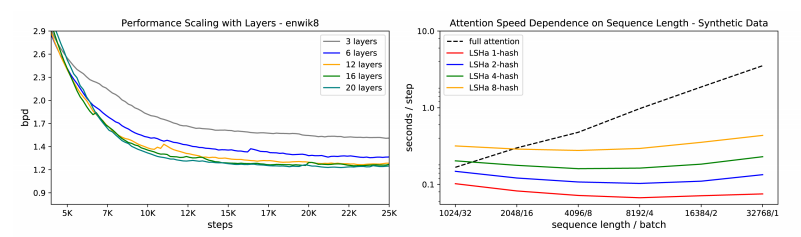
LSH Attention의 이득은 실제 소요시간을 측정할 때 더 두드러집니다. enwiki8에서 LSH Attention으로 계산하면 데이터 포인트의 길이가 길어져도 매 단계마다 소요시간이 거의 일정하나, Full Attention을 사용한 기존 모델에서는 선형으로 증가함을 알 수 있습니다. LSH Attention은 Layer를 많이 둘수록 더 높은 성능을 기록했지만, 개수가 12개를 넘어가면 성능향상폭은 미미하였습니다.

글을 마치며

논문의 저자들은 데이터 토큰의 길이에 따라 복잡도가 제곱으로 늘어나는 기존 모델의 문제점을 지적하였으며, LSH Attention과 그 외의 부차적인 테크닉을 활용하여 성능을 저하시키지 않으면서 선형적으로 복잡도를 개선할 수 있음을 보였습니다.

저는 논문을 보면서 다음처럼 생각했습니다. 하나는 기존의 Naive Transformer 모델이 Attention을 효과적으로 사용하지 못하므로 속도/크기/성능 면에서 최적화될 여지가 많다는 점입니다. 또 하나는 문장이나 문단 등의 짧은 단위에서는 기존 모델을 대체하기 어렵지만 문서나 책자 단위의 데이터를 다룰 때(예를 들면 질의 응답 시스템 등에서) 효과적으로 적용될 잠재력이 있다는 점입니다.

앞으로 데이터 모델은 어디까지 발전할까요? 그리고 그러한 데이터 모델은 또 어디까지 자연어처리 영역에 접목될까요? 그 답변을 찾아서 오늘도 핑퐁의 연구자들은 노력한답니다. 다음 블로그 글도 기대해주시면 감사하겠습니다.

Reference

Appendix

구면으로 사상할 때 임베딩의 크기 정보가 손실되는 문제에 대해서

Angular LSH를 사용하면 단위 구면에 사상하는 과정에서 임베딩의 크기(magnitude/norm) 정보가 손실됩니다. 그렇지만 실제로 NLP 어플리케이션을 만들다보면 임베딩 벡터의 크기는 그다지 중요하지 않음을 알게됩니다. 첫째로 Transformer의 출력은 각 층을 지나면서 Layer Normalization 연산을 이미 거쳤기 때문에 실제 임베딩의 크기 정보가 퇴색됩니다. 둘째로 임베딩에서 중요한 정보는 크기가 아니라 방향이기 때문입니다. 실제로 우리가 임베딩 간의 유사도를 측정할 때 방향 정보만 활용한 코사인 유사도를 보는 경우가 대부분입니다. Meng et al.은 이 점을 지적하면서 NeurIPS 2019에서 직교 공간(Euclidean Space)보다 구면 공간(Spherical Space)의 임베딩 표현이 더 성능이 우수함을 확인하였습니다.

LSH Attention의 유효성에 대해서

Hash값이 비슷한 데이터 포인트들끼리 attend를 하는 것만으로도 충분히 성능이 향상됨을 검증하기 위하여, 논문의 저자들은 다음의 합성 실험을 했습니다. 1~127 범위 내의 숫자 511개로 이루어진 고정된 문자열 w가 있다고 가정해봅시다. 논문의 저자들은 제안한 LSH Attention Transformer가 이 문자열을 반복할 수 있는지 확인하였습니다. 즉, 문자열 w에 대해서 w → 0 w 0 w 형태의 새 문자열을 출력하는 작업입니다. 각 Transformer의 Hash값 개수를 변형해가면서 정확도를 확인하였습니다.

모든 쌍을 고려한 Full Attention 모델은 Full Attention 모델로 테스트 했을 때만 성능이 높았습니다. 반면, LSH로 학습시킨 모델은 Full Attention 모델로 테스트했을 때의 성능은 크게 낮았지만 다른 LSH 모델로 테스트했을 때 성능이 우수했습니다. 결과가 시사하는 바는 크게 2가지입니다.

최소한 문자열을 복사하는 정도의 작업에는 모든 쌍의 정보가 사용되지 않아도 된다는 것입니다. RoBERTa 등 BERT의 후속 연구에서 밝힌 사실은 모델의 크기가 수행하는 작업에 비해 너무 크다는 것이었습니다. (Harder, Better, Faster, Stronger 글 을 참조해주십시오.) 위 실험 역시 그 가설을 어느 정도 증명합니다.
LSH와 Full Attention Transformer는 상당히 다른 방식으로 학습합니다. 이는 LSH 모델끼리 훈련하거나 실행할 때의 성능이 Full Attention 모델을 활용했을 때보다 우수한 것으로 증명됩니다. 만약 이 가설이 맞다면 원 Transformer 구조가 각 데이터 포인트 쌍의 영향력을 보다 밋밋하게 간주한다고 볼 수 있겠습니다.

꼼꼼하고 이해하기 쉬운 Reformer 리뷰

Table of Contents